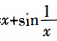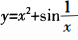题库

1.设函数f（x）在区间[-1，1]上连续，则x=0是函数g（x）=的是（）。

A.跳跃间断点

B.可去间断点

C.无穷间断点

D.振荡间断点

2.下列曲线中有渐近线的是（）。

A.y=x+sinx

B.y=x²+sinx

C.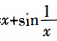

D.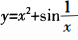

1.设位于曲线y=下方，x轴上方的无界区域为G，求G绕x轴旋转一周所得空间区域的体积。

2.若|f|或f2在I上连续那么f在I上是否必连续？如果是，说明理由；如果不是，举例说明。

1.设函数f（x）在[0，3]上连续，在（0，3）内存在二阶导数，且。 （1）证明存在η∈（0，2），使f（η）=f（0）； （2）证明存在ξ∈（0，3），使f"（ξ）=0。

1.在对学生进行数学学习评价时，既要重视学生知识、技能的掌握和能力的提高，又要重视其情感、态度和价值观的变化；既要重视学生学习水平的甄别，又要重视其学习过程中主观能动性的发挥；既要重视定量的认识，又要重视定性的分析；既要重视教育者对学生的评价，又要重视学生的自评、互评。对学生实施促进学生发展的多元化评价包括哪些方面？请给出一些评价的具体建议。

1.阅读《任意角的三角函数》教学片段，回答问题。 第一部分——情景引入 问题1：假设一个摩天轮的中心离地面的高度为b，它的直径为2R，逆时针方向匀速转动，转动一周需要360秒。若现在你坐在座舱中，从初始位置OA出发（如图1所示），过了30秒后，你离地面的高度h为多少？过了45秒呢？过了t秒呢？ 第二部分——引入新课 问题2：请问t的范围是什么？随着时间的推移，你离地面的高度h为多少？能不能猜想h=h0+R sint0？ 问题3：如图2建立直角坐标系，设点P（xp，yp），你能用直角坐标系中角的终边上的点的坐标来表示锐角α的正弦函数的定义吗？能否也定义其他三角函数（余弦、正切）？ 【学生自主探究】 问题4：改变终边上的点的位置，这三个比值会改变吗？为什么？ 【分析】先由学生回答问题，教师再引导学生选几个点，计算比值，获得具体认识，并由相似三角形的性质证明。 问题5：大家根据第一象限角的正弦函数的定义，能否也给出第二象限角的定义呢？ 【学生自主探究】学生通过上面已知知识得到。 学生定义好第二象限角后，让学生自己算出摩天轮座舱在第150秒时，离地面的高度h。 通过摩天轮知道：h=h0+Rsin150°=h1=h0+Rsin30°。 由此得到：sin150°=。 问题6：在第三象限或第四象限能成立吗？ 【教师总结】我们通过这个模型知道如何在某些范围内计算自己此时离地面的高度，用数学模型h=h0+ Rsint0来表示，当摩天轮转动时，角度的概念也不知不觉地推广到任意角，对于任意角的正弦不能只是依赖于角所在的直角三角形中的对边的长度比斜边长度了，应该用点P的横坐标来代替|MP|或-|MP|，这样就能够很好地表示出正弦函数任意角的定义。 问题： （1）阅读材料，简述教师选用摩天轮这一例子的意图； （2）简述教师设置一系列问题的作用。

1.《普通高中数学课程标准（实验）》关于等比数列前n项和的教学要求是通过学习公式的推导，发现公式的特点进而掌握公式的运用。 请基于该要求，完成下列教学设计任务： （1）设计等比数列前n项和的教学目标； （2）等比数列前n项和的教学重点以及难点； （3）设计等比数列前n项和的教学流程，使学生领悟教学过程中的数学思想方法。