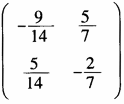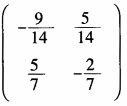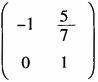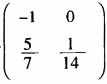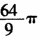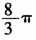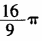题型介绍
一、单项选择题((本大题共40分,每小题5分。))
1.设,,则(AB)=( )。
A.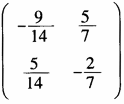
B.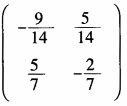
C.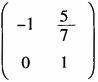
D.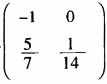
【正确答案-参考解析】:参加考试可见2.已知球面上过A、B、C三点的截面到球心的距离是球半径的一半,且AB=BC=CA=2,则球表面积是( )。
A.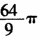
B.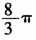
C.4π
D.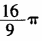
【正确答案-参考解析】:参加考试可见1.给出中学几何研究图形的几个主要方法,并试以其中一种为例,说明该种方法的基本特点。
【正确答案-参考解析】:参加考试可见1.设x,y∈R,A={a|a=x-3x+1},B={b|b=y+3y+1},求集合A与B之间的关系。
【正确答案-参考解析】:参加考试可见2.已知,,,求tan(α-2β)的值。
【正确答案-参考解析】:参加考试可见1.
Rt△ABC中,∠C=90°,BC=36,若平面ABC外一点P与平面A,B,C三点等距离,且P到平面ABC的距离PH为80,M为AC的中点。
(1)求证:PM⊥AC;
(2)求P到直线AC的距离;
(3)求PM与平面ABC所成角的正切值。
【正确答案-参考解析】:参加考试可见1.
正三棱柱ABC-ABC的底面边长为a,在侧棱BB上截取,在侧棱CC上截取CE=a,过A、D、E作棱柱的截面ADE。
(1)求△ADE的面积;
(2)求证:平面ADE⊥平面ACCA。
【正确答案-参考解析】:参加考试可见1.
请以"定义与命题"为课题,完成下列教学设计。
(1)教学目标。
(2)教学重点、难点。
(3)教学过程(只要求写出新课导入和新知探究、巩固、应用等)及设计意图。
【正确答案-参考解析】:参加考试可见