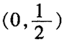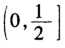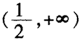题型介绍
一、单项选择题((本大题共40分,每小题5分。))
1.若定义在(-1,0)内的函数,则a的取值范围是( )。
A.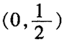
B.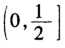
C.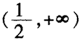
D.(0,+∞)
【正确答案-参考解析】:参加考试可见2.直线3x-4y-9=0与圆x+y=4的位置关系是( )。
A.相交且过圆心
B.相切
C.相离
D.相交但不过圆心
【正确答案-参考解析】:参加考试可见1.如何在数学教学中贯彻抽象与具体相结合的原则?
【正确答案-参考解析】:参加考试可见1.
已知△ABC中,A(2,-1),B(4,3),C(3,-2),求:
(1)BC边上的高所在直线方程;
(2)AB边中垂线方程;
(3)∠A平分线所在直线方程。
【正确答案-参考解析】:参加考试可见2.若实数a,b,c成等差数列,求直线族ax+by+c=0被圆x+y=5截得线段中点的轨迹方程。
【正确答案-参考解析】:参加考试可见1.
某同学在求反比例函数,当x≤3时,求y的取值范围时直接将x≤3代入,得。
问题:(1)该同学的解题过程哪步错了?分析原因;
(2)针对该生的情况,请你设计一个辅导教学片断,并说明设计意图;
(3)怎样防范这样的错误呢?
【正确答案-参考解析】:参加考试可见1.求的增减区间及极值。
【正确答案-参考解析】:参加考试可见1.
初中"两圆的公切线"设定如下教学目标:
(1)理解两圆相切长等有关概念,掌握两圆外公切线长的求法;
(2)培养学生的归纳、总结能力;
(3)通过两圆外公切线长的求法向学生渗透"转化"思想。
完成下列任务:
(1)根据教学目标,给出两个问题,并说明其设计意图。
(2)本节的教学重点是什么?
(3)作为初中阶段的重点内容,其难点是什么?
(4)给出一个教学活动设计。
【正确答案-参考解析】:参加考试可见