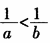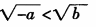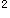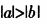题库

1.设a，b，c是任意的非零平面向量，且相互不共线，有以下结论①（a·b）·c-（c·a）·b=0；②|a|-|b|

A.①②

B.②③

C.③④

D.②④

2.如果a0，那么，下列不等式中正确的是（ ）。

A.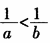

B.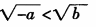

C.a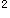

D.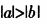

1.什么是解题方法多样化？解题方法的多样化有什么作用？谈谈如何促进解决问题方式的多样化。

1.如图，梯形ABCD中，AD∥BC，AB=DC，∠ADC=120°，对角线CA平分∠DCB，E为BC的中点，试求△DCE与四边形ABED面积的比。

2.已知数列中，a＝1，且 (1)求证：数列是等差数列； (2)求数列的通项公式。

1.以"三角形的中位线定理"教学为例，简述数学定理教学的主要环节。

1.已知是由非负整数组成的无穷数列，该数列前n项的最大值记为A，第n项之后各项a+1，a+2，…的最小值记为B，d＝A-B。 (1)若为2，1，4，3，2，1，4，3，…，是一个周期为4的数列(即对任意n∈N，a+4＝a)，写出d，d，d，d的值； (2)设d为非负整数，证明：d-d(n＝1，2，3...)的充分必要条件为为公差为d的等差数列； (3)证明：若a＝2，d＝1(n＝1，2，3，…)，则的项只能是1或者2，且有无穷多项为1．

1. 阅读下列教学片段。 呈现问题情境：某股民在上星期五以每股27元的价格买进某股票1000股。该股票的涨跌情况如下表(单位：元)。   师：星期四收盘时，每股多少元？ 提问生1、2(疑惑不解状)。  生3：27-2.5＝25.5(元)。 师：星期四收盘价实际上就是求有理数的和，应该为：27+4+4.5-1-2.5＝32(元)。  师：周二收盘价最高为35.5元；周五最低为26元。  师：已知该股民买进股票时付了3‰的交易税，卖出股票时需付成效额3‰的手续费和2‰的交易税，如果该股民在星期五收盘前将全部股票卖出，他的收益情况如何？ 提问生4、5(困惑状)。  生6：买入：27×1000×(1+3‰)＝27081(元)； 卖出：26×1000×(1+3‰+2‰)＝26130(元)； 收益：26130-27081＝-951(元)。 师：生6的解答错了，正确解答为： 买入股票所花费的资金总额为：27×1000x(1+3‰)＝27081(元)； 卖出股票时所得资金总额为：26×1000×(1-3‰-2‰)＝25870(元)； 上周交易的收益为：25870-27081＝-1211(元)，实际亏损了1211元。  师：请听明白的同学举手。 此时课堂上约有三、四个学生举起了手，绝大部分学生眼中闪烁着疑惑之意。有些学生在窃窃私语，有一学生轻声道："老师，我听不懂！"……少部分学生烦燥之意露于言表。  问题：(1)案例中老师犯了什么错误？ (2)该案例中学生的数学困惑是什么？  (3)该案例的启示是什么？