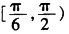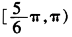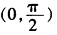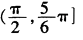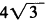题库

1.若，则直线2xcosα+3y+1=0的倾斜角的取值范围（ ）。

A.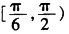

B.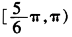

C.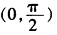

D.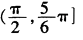

2.抛物线y=4x的焦点为F，准线为l，经过F且斜率为的直线与抛物线在x轴上方的部分相交于点A，AK⊥ι，垂足为K，则△AKF的面积是（ ）。

A.4

B.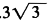

C.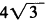

D.8

1.有位老师说，图形与几何这一部分的学习重点是培养学生的几何证明能力。谈谈你对这一观点的看法。

1.设矩阵,若存在一矩阵使得A=PBP。试求（1）矩阵B；（2）B。

2.求与直线及直线都平行且经过坐标原点的平面方程。

1. 下面为某校老师教授"等比数列"一节的教学片断：  环节一：举例引入等比数列的概念  环节二：等比数列概念的理解  环节三：类比等差数列通项公式的推导得等比数列的通项公式  环节四：学生自学例题并做练习  环节五：课堂小结和布置作业（剩余5分钟）  师：好了，我们这节课所研究的知识就到这里，接下来给大家一分钟的时间，请大家静静地回想这节课上我们学习了什么？你有什么样的收获？同时还存在哪些疑问？  师：我们来分享一下大家的收获，请问有哪位同学愿意和我们谈谈你有什么收获？  生甲：我这节课收获很大，首先我知道了什么样的数列是等比数列，其次懂得了等比数列的通项公式及其推导。  师：很好！甲同学收获确实很大啊！还有其他同学愿意分享自己的收获吗？  生乙：我还学会了用等比数列的定义、通项公式去解决一些简单的问题。  师：不错。还有吗？  生丙：学习了这节课，我学会了数学的类比思想，类比等差数列的知识来学习等比数列的知识。  师：很好！从这几位同学的发言中可以看出你们都有认真总结过这节课的知识！最后，课后研究作业是"报纸折叠38次的故事"，希望大家能用我们这节课所学的知识来理解一下这位数学家所说的话是否有他的道理？为什么？ 请你结合上述教学过程，分析一下这样的课堂小结有哪些优点或可改进的地方。

1. 已知f（x）是定义在（-1，1）的函数，并且满足下列条件： ①对都有f（x）+f（x）=成立； ②当x∈（-1,0）时,f（x）>0。 请回答下列问题：  （1）判断f（x）在（-1，1）上的奇偶性，并说明理由；  （2）判断f（x）在（0，1）上的单调性，并说明理由。

1.请你设计一个引入"圆与圆位置关系"的激趣情境，并写出设计意图。