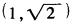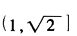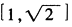题型介绍
一、单项选择题((本大题共40分,每小题5分。))
1.已知四点,无三点共线,则可以确定( )。
A.1个平面
B.4个平面
C.1个或4个平面
D.无法确定
【正确答案-参考解析】:参加考试可见2.在△ABC中,a,b,c分别是∠A,∠B,∠C所对应的边,∠C=90°,则的取值范围是( )。
A.(1,2)
B.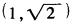
C.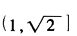
D.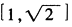
【正确答案-参考解析】:参加考试可见1.论述课堂教学改革的方向。
【正确答案-参考解析】:参加考试可见1.一圆与y轴相切,圆心在x-3y=0上,在y=x上截得的弦长为2,求圆的方程。
【正确答案-参考解析】:参加考试可见2.一商家销售某种商品的价格满足关系P=7-0.2x(万元/吨),其中x为销售量,该商品的成本函数为C=3x+1(万元)。
(1)若每销售一吨商品,政府要征税t万元,求该商家获最大利润时的销售量;
(2)t为何值时,政府税收总额最大?
【正确答案-参考解析】:参加考试可见1.某教师在进行二元一次方程教学时,给学生出了如下一道练习题:
已知a,b是方程x+(k-1)x+k+1=0的两个根且a,b是某直角三角形的两条直角边,其斜边长等于1,求k的值。
某学生的解答过程如下:
解:a,b是方程x+(k-1)x+k+1=0的两个根。
a+b=1-k,ab=k+1。
又由已知得:a+b=1,
(a+b)-2ab=1,即k-4k-2=0,解得k=2±
问题:
(1)指出该生解题过程中的错误,分析其错误原因;
(2)给出你的正确解答;
(3)指出你解题所运用的数学思想方法。
【正确答案-参考解析】:参加考试可见1.在△ABC中,已知A,B,C对应的边分别为a,b,c,且∠C=2∠A,cosA=,
(1)求cosC和cosB的值;
(2)当时,求a,b,c的值。
【正确答案-参考解析】:参加考试可见1.
针对初中数学"二元一次方程"的内容,完成下列任务。
(1)写出"二元一次方程"这节课的教学目标以及重难点。
(2)设计一个与二元一次方程有关的例题,并说明你的设计意图。
(3)举例写出几个适合本节课教学的教法和学法。
【正确答案-参考解析】:参加考试可见