题型介绍
1.x=0是的( )。
A.连续点
B.跳跃间断点
C.可去间断点
D.第二类间断点
【正确答案-参考解析】:参加考试可见1.已知函数f(x)=lg(x+1)。
(1)若0<f(1-2x)-f(x)<1,求x的取值范围;
(2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,有g(x)=f(x),求函数
y=g(x)(x∈[1,2])的反函数。
【正确答案-参考解析】:参加考试可见2.已知R的两组基a=(1,0,-1),α=(2,1,1),α=(1,1,1)与β=(0,1,1),β=(-1,1,0),β=(1,2,1)
(1)求由基α,α,α到基β,β,β的过渡矩阵;
(2)求γ=(9,6,5)在这两组基下的坐标;
(3)求向量δ,使它在这两组基下有相同的坐标。
【正确答案-参考解析】:参加考试可见1.设概率空间为Ω={1,2,3,4,5,6},且这六个数的出现概率均为。设事件A={1,3,5},事件B={1,2}。请回答事件A和B是否独立,并说明理由。
【正确答案-参考解析】:参加考试可见1.针对"一元二次方程"起始课的教学,两位老师给出了如下教学设计片段:
【教师甲】
设置问题:请同学们根据下列问题,只列出含未知数X的方程:
(1)一个正方形的面积为2,求正方形的边长X。
(2)长度为1的线段AB上有一点C,且满足,求线段AC的长X。
预设:学生会分别列出两个方程。
教师要求学生分别整理成方程左侧降幂排列,右侧为零的形式,然后引导学生完成下面两件事:对比"一元一次方程"的定义,为这类方程定义一个名称--一元二次方程。再请学生自行写出几个不同的一元二次方程,并提炼出一元二次方程的一般表达式。
【教师乙】
上课开始。提问:什么是"一元一次方程"?请你根据"一元一次方程"的定义,给出"一元二次方程"的定义,并举出几个"一元二次方程"的例子。在学生举例的基础上,提炼出"一元二次方程"的一般表达式。
请完成下列任务:
(1)请分析两位老师引入"一元二次方程"概念设计方案的各自的特点。
(2)在教学中,当引入一个新的数学概念之后,往往通过例题、习题加深对概念的理解。请针对"一元二次方程"概念,设计不同难度的两道例题和两道练习题,以加深学生对"一元二次方程"概念的理解。
【正确答案-参考解析】:参加考试可见
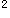 +y
+y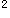 -10x+9=0
-10x+9=0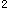 +y
+y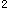 -10x+16=0
-10x+16=0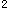 +y
+y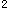 +10x+16=0
+10x+16=0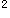 +y
+y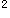 +10x+9=0
+10x+9=0