题型介绍
一、单选题((1)~(8)小题,每小题4分,共32分。下列每题给出的四个选项中,只有一个选项是符合题目要求的。)
1.n维向量组α1,α2,…,αm(3≤m≤n)线性无关的充分必要条件是()。
A.存在一组不全为零的数k1,k2,…,km,使k1α1+k2α2+…+kmαm≠0
B.α1,α2,…,αm中任意两个向量都线性无关
C.α1,α2,…,αm中存在一个向量,它不能由其余向量线性表示
D.α1,α2,…,αm中任何一个向量都不能由其余向量线性表示
【正确答案-参考解析】:参加考试可见2.设函数f(x)对任意x均满足等式f(1+x)=af(x),且有,其中a,b为非零常数,则()。
A.f(x)在x=1处不可导
B.f(x)在x=1处可导,且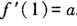
C.f(x)在x=1处可导,且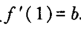
D.f(x)在x=1处可导,且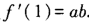
【正确答案-参考解析】:参加考试可见二、填空题((9)~(14)小题,每小题4分,共24分。)
1.设f(x)有一个原函数,则=______。
【正确答案-参考解析】:参加考试可见2.设a为n维单位列向量,E为n阶单位矩阵,则矩阵E-aaT的秩为______。
【正确答案-参考解析】:参加考试可见三、解答题1((15)~(19)小题,共50分。解答应写出文字说明、证明过程或演算步骤。)
1.设x≥0,证明。
【正确答案-参考解析】:参加考试可见2.设是方程y’’+y=0的满足条件y(0)=0,y’(0)=1的解,证明方程y’’+y=f(x)满足条件y’(0)=0的解为。
【正确答案-参考解析】:参加考试可见四、解答题2((20)~(23)小题,共44分。解答应写出文字说明、证明过程或演算步骤。)
1.已知α1,α2,α3,α4是线性方程组Ax=0的一个基础解系,若β1=α1+tα2,β2=α2+tα3,β3=α3+tα4,β4=α4+tα1,讨论实数t满足什么关系时β1,β2,β3,β4线性无关。
【正确答案-参考解析】:参加考试可见2.给定椭球体在第一象限的部分。 (1)求椭球体上任意点处椭球面的切平面。 (2)在何处的切平面与三个坐标面围成的空间区域的体积最小。
【正确答案-参考解析】:参加考试可见